EQUAÇÃO DO 1º E DO 2º GRAU
Professor Diminoi
Questões de equações do 1º grau
Alternativa: D
(a) Aplicando a fórmula de Bhaskara, resolva a seguinte equações do 2º grau 3x² – 7x + 4 = 0.
Vamos aplicar esses coeficientes na fórmula de Bhaskara:
Soma e Produto
Professor Diminoi
Questões de equações do 1º grau
Alternativa: D
(a) Aplicando a fórmula de Bhaskara, resolva a seguinte equações do 2º grau 3x² – 7x + 4 = 0.
Vamos aplicar esses coeficientes na fórmula de Bhaskara:
Soma e Produto
- INICIO
- ENEM
- UNIVERSIDADES
- VESTIBULAR
- VESTIBULANDO
- MATEMÁTICA EF & EM
- ATIVIDADES ESCOLARES - 2021/2022/2023/2024
- PEI
- SE/SP
- VESTIBULINHOS
- ELETRICIDADE
- ONDULATÓRIA
- ÓPTICA
- MAGNETISMO
- ACUSTICA
- ASTRONOMIA
- FORMULAS E EQUAÇÕES - [A]
- FORMULAS E EQUACOE - [B]
- ENERGIA E SUAS TRANSFORMAÇÕES
- FÍSICA - [ Vídeo ]
- HORA DE ESTUDAR [ FÍSICA]
- FIES / SISU / ProUni / PRONATEC
- PROVAS E GABARITOS
- ESTUDE PARA O VESTIBULAR
- FÍSICA DE PARTÍCULA - [PESQUISA]
- NOTAÇÃO CIENTÍFICA
- FISICA - ENEM
- FISICA MODERNA
- CINEMATICA
- CINEMÁTICA-MU/MUV-M. PROGRESSIVO E RETROGAD
- TERMOLOGIA
- DINÂMICA II
- ESTÁTICA DOS SÓLIDOS
- MECÂNICA
- HIDROSTÁTICA
- CANAL DO EDUCADOR
- VESTIBULANDO
- MATEMÁTICA - ENSINO MÉDIO
- PORCENTAGEM
- GRÁFICOS I
- GEOMETRIA PLANA III
- GEOMETRIA ESPACIAL II
- EQUAÇÃO DO 1º E DO 2º GRAU
- PLANO CARTSIANO I
- PA & PG
- FUNÇÃO/COEFICIENTE LINEAR/ANGULA E EQUAÇÃO DA RETA
- PONTO/RETA/ALINHAMENTO
- MATRIZES
- REGRA DE TRES GRANDEZA DIRA/INVRS
- FRAÇÃO
- MMC e MDC
- EXPRESSÕES NUMÉRICAS I
- RADICIAÇÃO POTENCIAÇÃO
- ATRIBUIÇÕES DO QUANDO DO MAGISTÉRIO
- ORGANIZAÇÃO CURRICULAR
- QUESTÕES DE MATEMATCA - 9º ANO
- EQUANCÃO DO 2º GRAU - 9º ANO
- MATEMÁTICE 9 ANO BLOG - PEI TEREZA DELATA
- MATEMÁTICA - E. FUNDAMENTAL
- GEOMETRIA GERAL - EF
- CONJUNTOS NUMÉRICOS
- POLÍGONO
- CIRCULOS, CIRCINFERENCIAS E ARCOS
- VISTAS ORTOGONIAS DE FIGURAS ESPECIAIS
- PROBABILIDADE, PERMUTAÇÃO, ARRANJOS E FATORIAL
- ESTATÍSTICA
- AAP/VESTIBULINHOS
- QUARENTENA - 7 ANO
- PARTE DIVERSIFICADA DO CURRICULO
- MATEMÁTICA & ENEM II
- ORIENTAÇÃO DE ESTDUDOS
- MATEMÁTICA FINACEIRA I
- QUARENTENA - PARTE DIVERSIFICADA
- PLANIFICACAO DE SOLIDOS GEOMATRICOS
- AULA REMOTAS - 2021
- FISICA - 3ª SERIE
- FISICA - 2ª SERIE
- TEOREMA DE PITÁGORAS
- FRAÇÃO GERATIZ
- ADR/AAP/SEQUENCIA DIDÁTICA
- Números decimais
- POLINÔMIOS
- POLINÔMIO-EF
- POLINÔMIOS E PRODUTAS NOTÁVEIS
- MATRIZES ENERGÉTICA
- PROBLEMAS MATEMÁRICOS
- PROVAS TERMOMECÂNICA
- PROVA SENAI
- PROVAS ETEC
- PROVAS ENEM
- QUESTÕES SARESP
- PROVAS AAP/ADE
- TEOREMA DE TALES & PROPORCIONALIDADE
- GRANDEZA/RAZÃO/PROPORÇÃO
- PEI Tereza Delta - Atividades 2021
- PROBABILIDADE - ESTATISTICA
- MATEMÁTICA E SUAS HABILIDADES
- FATORACAO
- FRAÇÃO E NÚMEROS MISTOS
- ANÁLISE COMBINATÓRIA/A
- CMSP & AVALIAÇÕES EXTERNAS
- PROVAS ENEM COMENTADA
- DOCUMENTOS - PEI
- OBMEP
- POLINÔMIO & FATORAÇÃO ALGÉBRICA
- NIVELAMENTO / RECUPERAÇÃO / REFORÇO
- QUSTÕES - ETEC
- QUESTÕES DO SARESP
- QUESTÕES - TERMOMECANICA
- QEUSTÕES PROVA BRASIL
- QUESTÕES SENAI
- QUESTÕES JUROS SIMPLES
- QUESTÕES - JUROS COMPOSTOS
- ESTATISTICA GERAL
- UNIDADE DE MEDIDA
- DIVISAO/MULTIPLICACAO/SOMA/SUBTRACAO
- MMC & MDC
- EXPRESSAO NUMERICA
- NUMEROS DECIMAIS
- NOTACAO CIENTIFICA 1
- RAIZ QUADRADA & RAIZ CUBICA
- DIZIMA PERIODICA
- PRODUTOS NOTAVIES
- CIRCUNFERENCIA
- GRANDEZA DIRETAMENTE & INVERSAMENTE PROPORCIONAL
- TERMOMECANICA/2022 - MATEMÁTICA
- FRACAO 2022
- EXPRESSAO DO 1º GRAU
- EQUACAO DO 2º GRAU
- LOGARITMO
- NUMEROS MISTOS E/OU FRACOES IMPROPRIAS
- FRACAO GERATRIZ
- PROPRIEDADES DA POTENCIACAO
- OPERACOES COM RADICAIS
- MODULO DE UM NUMERO
- EF II - FRACAO
- EF II - ALGARISMOS ROMANO
- EF II - ANGULOS
- EF II - EQUACAO DO 2º GRAU
- EF II - EQUACAOES DO 1º GRAU COM UMA VARIAVEL
- EF II - EQUACAOES DO 1º GRAU COM DUAS VARIAVEL
- EF II - GEOMETRIA PALNA
- EF - GRANDEZAS PROPORCIONAIS
- EF - INEQUACAOES DO 1º GRAU
- EF II - DIVISIBILIDADE
- EF - DIZIMA PERIODICA
- EF II - MEDIAS
- EF II - MEDIDAS DE CAPACIDADE
- EF II - MEDIDAS DE COMPRIMENTO
- EF II - MEDIDAS DE TEMPO
- EF II - MEDIDAS DE VOLUME
- EF II - MEDIDAS DE SUPERFICIES
- EF II - MEDIDAS DE MASSA
- EF II - POTENCIACAO
- EF II - POCENTAGEM
- EF II - NUMEROS DECIMAIS
- EF II - OPERACOES COM NUMEROS RACIONAIS DECIMAIS
- EF II - PROPORCAO
- EF II - SEMALHANCA DE POLIGONO
- EF II - REGRA DE TRES
- EF II - RAZAO
- EF II - RAZOES TRIGONOMETRICAS
- EF II - QUADRILATEROS
- EF II - RADICIACAO
- MATEMATICA - E. FUNDAMENTA II
- EM - ANALISE COMBINATORIA
- EM - BINOMIO DE NEWTON
- EM - DETERMINANTE
- EM - EQUACOES TRIGONOMETRICA
- EM - FUNCAO DO 1º OU FUNCAO AFIM
- EM - FUNCAO QUADRATICA
- EM - FUNCAO
- EM - GEOMETRIA ANALITICA – CIRCUNFERENCIA
- MATEMATICA - ENSINO MEDIO
- EM - GEOMETRIA ANALITICA – CONICAS
- EM - GEOMETRIA ANALITICA – RETAS
- EM - GEOMETRIA ESPACIAL
- EM - POLINOMIO
- EM - INEQUACOES TRIGONOMETRICAS
- EM - LOGARITMO
- EM - MATEMATICA FINANCEIRA
- EM - MATRIZES
- EM - NUMEROS COMPLEXOS
- EM - PROBABILIDADE
- EM - PROGRESSAO
- EM - SISTEMA LINEARES
- EM - TEORIA DOS CONJUNTOS
- EM - VETORES
- EM - CONJUNTOS NUMÉRICOS
- ENEM 2022 - PARTE I
- ENEM 2022 - PARTE II
- ENEM 2022 - PARTE III
- ENEM 2022 - PARTE IV
- REGRA DE TRÊS COMPOSTA
- FUVEST 2023 - PARTE I
- FUVEST 2023 - PARTE II
- SEQUÊNCIA NUMÉRICA - PA & PG
- SEQUÊNCIA NUMÉRICA - PA & PG - I
- PROBABILIDADE
- LEITURA E INTERPRETAÇÃO DE TEXTO I
- INTERPRETAÇÃO DE TEXTO II
- LEITURA E INTERPRETAÇÃO DE TEXTO III
- INTERPRETAÇÃO DE TEXTO - PRPOV BRASIL - 9º ANO
- PROVINHA DE PORTUGUES
- PROVA PAULISTA 1ºBim/2023-HISTORIA 6
- PROVA PAULISTA -1ºBim/2023-GEOGRAFIA 6
- PROVA PAULISTA 1ºBim/2023-CIEÊNCIAS 9
- PROVA PAULISTA -1ºBim/2023-HISTÓRIA 9
- PROVA PAULISTA -1ºBim/2023-GEOGRAFIA 9
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 9
- PROVA PAULISTA-1ºBim/2023-M-G-H-9
- PROVA PAULISTA 1ºBim/2023-HISTÓRIA 7
- PROVA PAULISTA 1ºBim/2023-CIENCIAS 7
- PROVA PAULISTA 1ºBim/2023-GEOGRAFIA 7
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 7
- PROVA PAULISTA- 1ºBim/2023-M-G-H-7
- PROVA PAULISTA-1ºBim/2023-M-G-H-C-8
- PROVA PAULISTA 1ºBim/2023-CIENCIAS 8
- PROVA PAULISTA 1ºBim/2023-HISTORIA 8
- PROVA PAULISTA 1ºBim/2023-GEOGRAFIA 8
- PROVA PAULISTA 1ºBim/2023-PORTUGUES 8
- PROVA PAULISTA-1ºBim/2023-M-G-H-C-6
- PROVA PAULISTA -1ºBim/2023-PORTUGUES 6
- PROVA PAULISTA -1ºBim/2023-CIENCIAS 6
- PROVA PAULISTA-MAT/GEO/HIT-2ºBIM/2023-8ºANO
- PROVA PAULISTA-MAT/GEO/HIS-2º BIM/2023-6ºANO
- PROVA PAULISTA-MAT/GEO/HIS-2º BIM/2023-7º ANO
- PROVA PAULISTA-MAT/GEO/HIS-2ºBIM-8ºANO-2023
- PROVA PAULISTA-MAT/GEO/HIS-2ºBIM/2023-9ºANO
- PROVA PAULISTA-LPT/ING/CIE-2ºBIM-6ºANO/2023
- PROVA PAULISTA-LPT/ING/CIE-2ºBIM-7ºANO/2023
- PROVA PAULISTA-LPT/ING/CIE-2ºBIM-8ºANO/2023
- PROVA PAULISTA-LPT/ING/CIE-2ºBIM-9ºANO/2023
- PP-M-1ª-1ºBIM-2023
- PP-M-2ºBim-1ª-2023
- PP-M-3ª-1ºBIM-2023
- PP-M-1ª-2ºBIM-2023
- PP-M-2ª-2ºBIM-2023
- PP-M-2ºBim-3ª-2023
- FUNÇÃO E.FUNDAMENATL - II
- FUNCAO LOGARITMICA E TRIGONOMETRICA
- PROPRIEDADES DA POTENCIAÇÃO - EF
- MONÔMIOS & EXPRESSÕES ALGÉBRICAS
- P.P-MAT/GEO/HIS-3ºB-9ºANO-2023
- PP-LPT/ING/CIE-3ºB-9ºANO/2023
- P.P-MAT/GEO/HIS-3ºB-6ºA/2023
- P.P-LPT/ING/CIE-3ºB-6ºA-2023
- P.P-MAT/GEO/HIS-3ºB-7ºA/2023
- P.P-LPT/ING/CIE-3ºB-7º A-2023
- P.P-MAT/GEO/HIS-3ºB-8ºANO/2023
- P.P-LPT/ING/CIE-3ºB-8ºA-2023
- MONOMIOS
- TERMOMECANICA VESTIBULINHO 2024
- ENEM 2023-1ºDIA
- ENEM 2023-2ºDIA
- FUVEST 2024
- ETEC - 1º Semestre/2024
- 1ªEM-Matemática, Ciências Humanas e Redação
- 1ªEM-Linguagens e Códigos Ciências da Natureza
- 2ªEM-Matemática, Ciências Humanas e Redação
- 2ªEM-Linguagens e Códigos Ciências da Natureza
- 3ºEM-Matemática, Ciências Humanas e Redação
- 3ªEM-Linguagens e Códigos Ciências da Natureza
- SIMULADO SARESP 9ºANO - PORTUGUÊS
- SIMULADO SARESP 9º - CIÊNCIAS DA NATUREZA
- SIMULADO SARESP 9º - CIÊNCIAS DA HUMANAS
- SIMULADO SARESP 9ºANO - MATEMÁTICA
- SARESP-GEO&HIST-EF&EM
- SARESP-MATEMÁTIC/EM
- MOVIMENTO UNIFORME - (MU)
- MOVIMENTO UNIFORMEMENTE VARIADO (MUV)
- MOVIMENTO PROGRESSIVO OU TRETRÓGRADO
- IMPULO/QUANTIDADE DE MOVIMENT0/COLISÃO
- DINAMICA I
- FISICA - ENEM/VESTIBULAR
- RAZAO E PROPOCAO
- ALBERT EINSTEIN
- PROPRIEDADES DA POTENCIACAO
- Área Reservada
- LIVRO DE FÍSICA
|
5 |









.gif)
.gif)
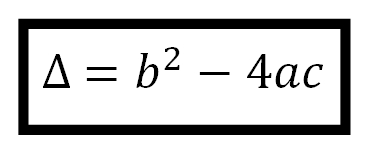
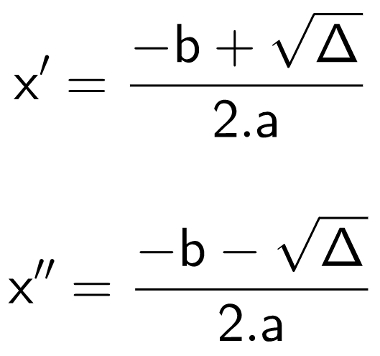
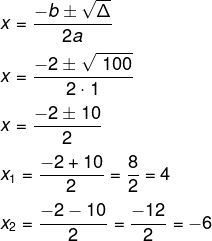
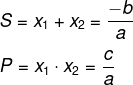
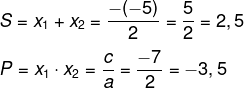
.jpg)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
